支持力の計算
表面波探査法により地盤の速度値を得ることができます。表面波速度値は他の工学的な地盤定数と良好な相関関係にあることから、一軸圧縮強さ等に換算することができます。このようにして、種々地盤定数を算定して支持力計算を行います。
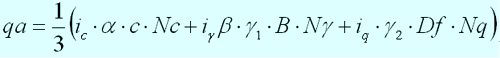
※支持力の計算は、国土交通省告示1113号の支持力計算式に準拠しています。

本来、土質の粘着力cや内部摩擦角φといった値は、ボーリングを行いサンプルを取り、室内試験などを行ったうえで得られるものです。表面波探査法は地盤の速度値及び層境界の情報を得ることができますが、土質については表面波探査法のデータから判断することは出来ません。現場の観察、既存資料などから、調査地が砂地盤であるのか、粘性土地盤であるのかを区別します。
粘性土地盤の場合
粘性土地盤の場合の支持力の計算方法
a. 粘性土地盤の場合
粘性土とは、土質分類法により細粒土として分類され、75μm以下の細粒分含有量が50%以上の土を対象として、シルト・粘土・砂混じりシルト・砂混じり粘土・関東ロームなどが分類されています。
当社では粘性土地盤における支持力の算出にあたり、内部摩擦角をφ=0°としています。
従って、粘性土地盤においては、粘着力cだけを考慮し計算していきます。
| 項目 | 数値 |
|---|---|
| 粘着力(c) | 表面波速度より一軸圧縮強度を算出 一軸圧縮強度より粘着力を算出 |
| 基礎の形状係数(α,β) | 長辺、短辺の長さに応じて決定する |
| 支持力係数 (Nc, Ny, Nq) |
内部摩擦角φ=0° Nc = 5.1 Ny = 0.0 Nq = 1.0 |
※建物形状が不明である場合、形状係数は最小値(α=1.0、β=0.3)を用いて計算します。
砂質地盤の場合
砂質地盤の場合の支持力の計算方法
b. 砂質地盤の場合
当社では砂質地盤における支持力の算出にあたり、粘着力をc = 0としています。従って、砂質土地盤においては、内部摩擦角φだけを考慮し、支持力の計算を行っています。
| 項目 | 数値 |
|---|---|
| 内部摩擦角(φ) | 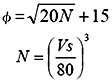 ※1 ※1 |
| 基礎の形状係数(α、β) | 長辺、短辺の長さに応じて決定する |
| 支持力係数 (Nc, Nr, Nq) |
内部摩擦角に応じて決定する※2 |
※1 道路橋示方書より
※2 建築基礎構造設計指針より
沈下量の予測計算
沈下量は即時沈下量 と圧密沈下量 の合計量として算出しました。予定されている構造物の形状及び重量により、地盤がどのくらい沈下する可能性を有しているのかを算出します。
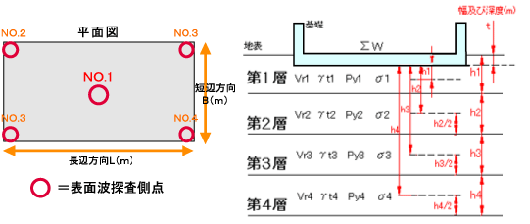
| t(m) | 地表から基礎底までの深さ |
|---|---|
| ∑W(kN/㎡) | 単位堆積あたりの荷重 |
| L(m) | 基礎の長辺方向長さ |
| B(m) | 基礎の短辺方向長さ |
| γtn(kN/㎥) | 各層の密度(表面波探査法や既存資料より) |
| Vr(m/s) | 各層の速度(表面波探査法による測定値) |
| Pyn(kN/㎡) | 各層の圧密降伏応力(表面波探査法測定値から換算) |
| σn(kN/㎡) | 各層の有効地中応力 |
| ⊿σn(kN/㎡) | 各層の荷重により増加すると想定される地中応力 |
| hn(m) | 各層厚(表面波探査法による測定値) |
| hn’(m) | 各層の中心までの深度 |
| ν | 地盤のポアソン比 |
| E(kN/㎡) | 地盤のヤング率 |
| G(kN/㎡) | 地盤の剛性率 |
計算式手順
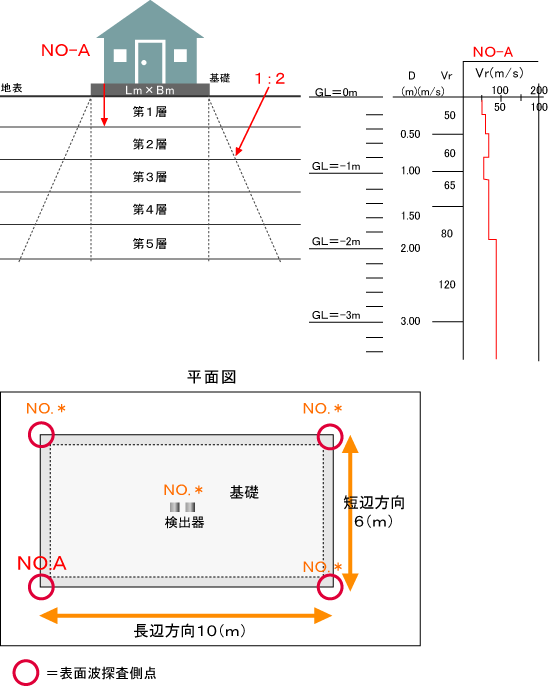
[a] 表面波探査法の結果から、深度方向の層境界深度及び各層の表面波速度値Vr がえられます。
得られた表面波速度値VrをS波速度Vsに換算します。
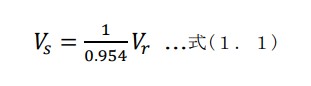
※計算式は 『土と基礎の振動』 F.E.リチャード他著より
[b] Vsより弾性係数(地盤の剛性率G、ヤング率E)を求めます。
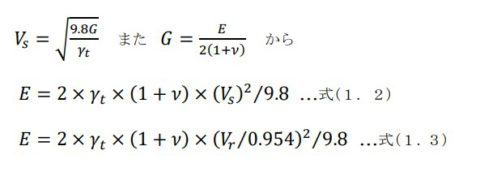
※計算式は 『地盤・基礎構造物の耐震設計』 地盤工学会より
[c] [b]で求めたヤング率E に対して、ひずみレベル補正を行います。
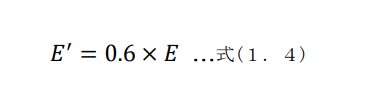
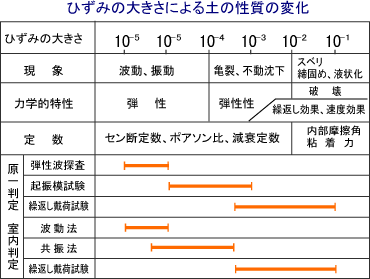
土質の動的な性質は、そのひづみ量に応じて変化します。表面波探査法による波動の伝播時に生ずる地盤のひずみと、建物などの建築により生じた地盤の沈下の際のひずみの量は大きな違いがあります。
このひずみの違いは弾性係数Eあるいは剛性率Gなどに著しい影響を及ぼします。(参考文献として、[土質動力学の基礎 石原研而著]、[建築基礎構造設計指針 日本建築学会編]など)
これらに考え基づき、ひずみレベルによる補正を行います。上図のなかで、表面波探査法は弾性波探査、あるいは起振機試験に相当します。ここから表面波探査法のひずみレベルは1×10-5であるものとします。同様に沈下の際の歪を1×10-3であるものとします。
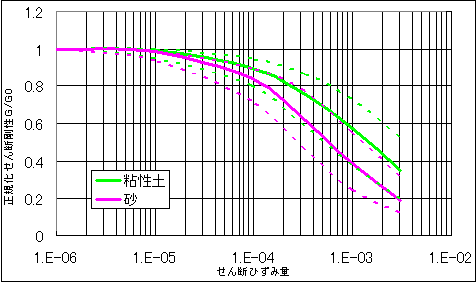
[d] S波探査法速度値Vs から、圧密降伏応力Py に換算します。
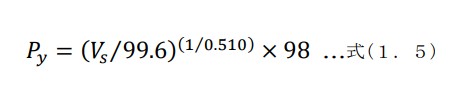
※計算式1.9は 『土質調査法』 土質工学会より
[e] 即時沈下量SE を求めます。
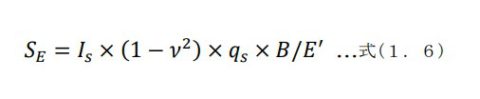
ここで
| qs(kN/㎡) | 加えられた荷重 |
| Is | 沈下係数(基礎の長辺L及び短辺Bにより決定、下表-1.1参照) |
| E’(kN/㎡) | 歪レベル補正を行った後の弾性係数 |
| B(m) | 基礎の短辺方向長さ |
| ν | 地盤のポアソン比 |
※[式1.6は建築基礎構造設計指針 日本建築学会より]
表‐1.1 沈下係数(L/Bと沈下係数Is の関係)
基礎が長方形の場合

基礎が正方形、あるいは円の場合
| 形状 | 基礎の剛性 | 底面上の位置 | 形状係数Is |
|---|---|---|---|
| 円 | 0 | 中央 | 1.00 |
| 辺 | 0.64 | ||
| ∞ | 全体 | 0.79 | |
| 正方形 | 0 | 中央 | 1.12 |
| 隅角 | 0.56 | ||
| 辺中央 | 0.77 | ||
| ∞ | 全体 | 0.88 |
※[表‐1.1は土質力学 足立格一郎著より]
[f] 圧密沈下量Sc を求めます。
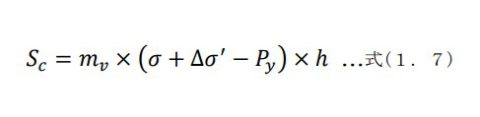
ここで
| ⊿σ’(kN/㎡) | 載荷重による増加地中応力 |
| σ(kN/㎡) | 土要素の地中応力 |
| h(m) | 地盤の層厚 |
| mν(㎡/kN) | 体積圧縮係数。収束時に限定し、 |
※体積圧縮係数mνは、土の圧縮性を示す係数です。mνは定数であり、土を弾性体であると想定すると、
ε=mν⊿σ’と考えることができます。(ε:ひずみ)。
[式1.7は、建築基礎構造設計指針 日本建築学会、土質力学 足立格一郎著より]
⊿σ’の計算方法については以下のように1:2の広がりをもって応力が分散しているものとして計算しています(建築基礎構造設計指針より)。ただし、計算者がニューマークの図表やブーシネスク式を用いることでも沈下量予測値を算出することは可能です。
[g] 合計の沈下量予測値S を算出します。
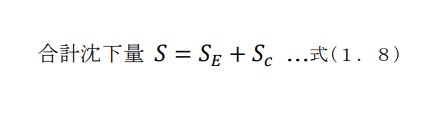
第1層目
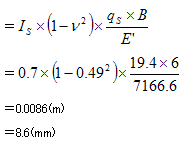
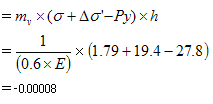
マイナスになることから、圧密沈下量は0cmという結果となります。
第2層目
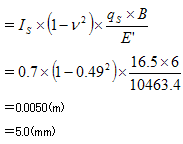
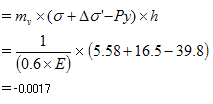
マイナスになることから、圧密沈下量は0cmという結果となります。
第3層目
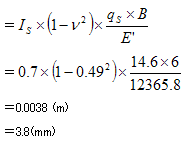
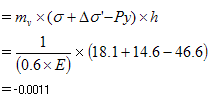
マイナスになることから、圧密沈下量は0cmという結果となります。
第4層目
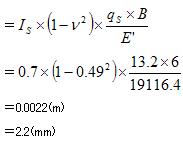
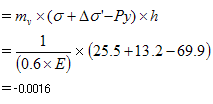
マイナスになることから、圧密沈下量は0cmという結果となります。
第5層目
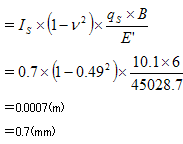
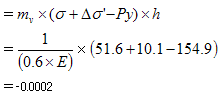
マイナスになることから、圧密沈下量は0cmという結果となります。
| 第1層目 | 即時沈下量SE+圧密沈下量Sc=8.6mm |
| 第2層目 | 即時沈下量SE+圧密沈下量Sc=5.0mm |
| 第3層目 | 即時沈下量SE+圧密沈下量Sc=3.8mm |
| 第4層目 | 即時沈下量SE+圧密沈下量Sc=2.2mm |
| 第5層目 | 即時沈下量SE+圧密沈下量Sc=0.7mm |
| 合計 | 20.3mm |



